|
|
|
---
|
|
|
|
title: Two-Loop Self-Energies and Tadpoles
|
|
|
|
permalink: /Two-Loop_Self-Energies_and_Tadpoles/
|
|
|
|
---
|
|
|
|
# Two-Loop Self-Energies and Tadpoles
|
|
|
|
|
|
|
|
|
|
|
|
[Category:Calculations](/Category:Calculations "wikilink")
|
|
|
|
|
|
|
|
General
|
|
|
|
-------
|
| ... | ... | @@ -26,12 +23,11 @@ Effective potential calculation |
|
|
|
|
|
|
|
We consider a set of real scalars {*ϕ*<sub>*k*</sub>} which are diagonalised to physical states {*h*<sub>*k*</sub>}. The scalar potential at tree-level is *V*<sup>*T*</sup>({*ϕ*<sub>*k*</sub>}). The pole masses of *h*<sub>*i*</sub> are in general the eigenvalues of the loop corrected mass matrix given by
|
|
|
|
|
|
|
|
$\\frac{\\partial^2 V^T}{\\partial \\phi_i \\partial \\phi_j} + \\sum_n \\Pi^{(n)}_{ij}(p^2)$
|
|
|
|
$`\frac{\partial^2 V^T}{\partial \phi_i \partial \phi_j} + \sum_n \Pi^{(n)}_{ij}(p^2)`$
|
|
|
|
|
|
|
|
Here, *Π*<sup>(*n*)</sup>(*p*<sup>2</sup>) is the self-energy at the *n*-loop level which usually depends on the external momenta. The parameters appearing in *V*<sup>*T*</sup> should be chosen to minimise the effective potential. For a pole mass *m*<sub>*h*<sub>*i*</sub></sub> the momentum is fixed to be *p*<sup>2</sup> = *m*<sub>*h*<sub>*i*</sub></sub><sup>2</sup>. To include this momentum dependence of *Π*<sup>(*n*)</sup> a diagrammatic calculation is necessary. However, things become significantly easier if one considers the limit of *p*<sup>2</sup> = 0. In this limit *Π*<sup>(*n*)</sup>(0) is equivalent to the second derivative of the effective potential at the *n*-loop level,
|
|
|
|
|
|
|
|
$\\label{eq:effpotApprox}
|
|
|
|
\\Pi_{ij}^{(n)}(0) = \\frac{\\partial^2 V^{(n)}}{\\partial \\phi_i \\partial \\phi_j} \\, .$
|
|
|
|
$` \Pi_{ij}^{(n)}(0) = \frac{\partial^2 V^{(n)}}{\partial \phi_i \partial \phi_j} \, .`$
|
|
|
|
|
|
|
|
SARAH/SPheno uses a hybrid method for the calculation of the scalar masses at the two-loop level in the *D**R*′ renormalization scheme: while the one-loop corrections are calculated including the full momentum dependence, the two-loop corrections are derived in the effective potential approximation.
|
|
|
|
|
| ... | ... | @@ -39,26 +35,23 @@ SARAH/SPheno uses a hybrid method for the calculation of the scalar masses at th |
|
|
|
|
|
|
|
CP-violating is neglected in the following. Therefore, a set of neutral, complex scalars *H*<sub>*i*</sub> are decomposed after symmetry breaking as
|
|
|
|
|
|
|
|
$H_i = \\frac{1}{\\sqrt{2}}\\left(\\phi_i + i \\sigma_i + v_i \\right) \\, .$
|
|
|
|
$`H_i = \frac{1}{\sqrt{2}}\left(\phi_i + i \sigma_i + v_i \right) \, .`$
|
|
|
|
|
|
|
|
*ϕ*<sub>*i*</sub> are the CP-even components, *σ*<sub>*i*</sub> the CP-odd ones and *v*<sub>*i*</sub> are the vacuum expectation values (VEVs). Under this assumption, the two-loop corrections to the mass matrix of real scalars in the effective potential approach are given by
|
|
|
|
|
|
|
|
$\\label{eq:Pi2L}
|
|
|
|
\\Pi^{(2)}_{ij}(0) = \\frac{\\partial^2 V^{(2)}}{\\partial v_i \\partial v_j}\\,.$
|
|
|
|
$` \Pi^{(2)}_{ij}(0) = \frac{\partial^2 V^{(2)}}{\partial v_i \partial v_j}\,.`$
|
|
|
|
|
|
|
|
In addition, one requires the tadpole contributions which are the first derivatives of the effective potential,
|
|
|
|
|
|
|
|
$\\label{eq:Ti2L}
|
|
|
|
\\delta t_i^{(2)} = \\frac{\\partial V^{(2)}}{\\partial v_i} \\,.$
|
|
|
|
$` \delta t_i^{(2)} = \frac{\partial V^{(2)}}{\partial v_i} \,.`$
|
|
|
|
|
|
|
|
The tadpoles then also contribute to the scalar masses by shifting the parameters; for example if we treat the vevs *v*<sub>*i*</sub> as fixed, “all-loop” correct values, then one can exchange them for scalar mass-squared at a given loop order via the tadpole equations, and in turn find compact equations for the total shift in the mass-squareds of
|
|
|
|
|
|
|
|
$\\begin{aligned}
|
|
|
|
\\big( \\Delta \\mathcal{M}^2_S \\big)_{ij}^{\\rm eff} =& \\frac{\\partial^2 V^{(2)}}{\\partial v_i \\partial v_j} -\\frac{\\delta_{ij}}{v_i} \\frac{\\partial V^{(2)}}{\\partial v_i },\\end{aligned}$ However, this is not done by SARAH which instead solves the tadpole equations and then uses the parameters derived from these in the tree-level mass calculation. The reason is that SARAHallows for a more general choice of variables to solve for via the tadpole equations.
|
|
|
|
$` \big( \Delta \mathcal{M}^2_S \big)_{ij}^{\rm eff} = \frac{\partial^2 V^{(2)}}{\partial v_i \partial v_j} -\frac{\delta_{ij}}{v_i} \frac{\partial V^{(2)}}{\partial v_i },`$ However, this is not done by SARAH which instead solves the tadpole equations and then uses the parameters derived from these in the tree-level mass calculation. The reason is that SARAHallows for a more general choice of variables to solve for via the tadpole equations.
|
|
|
|
|
|
|
|
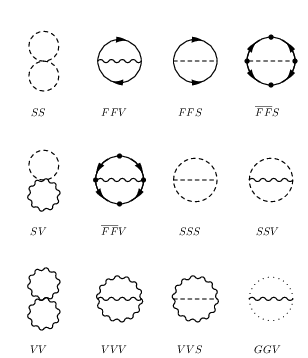
*V*<sup>(2)</sup> receives contributions from the possible topologies:
|
|
|
|
|
|
|
|
[comment]: <> [rahmenlos|zentriert](/Datei:Diagrams.png "wikilink")
|
|
|
|

|
|
|
|
|
|
|
|
<center>
|
|
|
|
|
| ... | ... | @@ -66,9 +59,9 @@ $\\begin{aligned} |
|
|
|
|
|
|
|
The generic results for all of these diagrams in Landau gauge have been presented in Ref. and SARAH makes heavily use of these results. However, not all topologies are implemented so far but *V**V*, *V**V**S*, *V**V**V*, *S**V*, and *G**G**V* are neglected. The reason is that these only lead to non-zero contributions if massive vector bosons are involved. Working in the gaugeless limit, all contributions stemming from broken gauge groups are neglected so far because of the many complications that they entail.
|
|
|
|
|
|
|
|
The remaining topologies are those which have been considered so far in the MSSM to obtain the dominant two-loop corrections and which are implemented in public computer tools. The impact on the Higgs mass is considered to be moderate when neglecting contributions propotional to the electroweak gauge couplings in models with the SM gauge sector, since they are significantly smaller than the strong and top Yukawa coupling – and the diagrams involving these couplings are of typically lower multiplicity. In fact, by inspecting the form of the loop functions it is evident that the topologies *S**V*, *V**V*, *V**V**V*, *V**V**S* < *m**a**t**h* > *a**n**d* < *m**a**t**h* > *G**G**V* lead to contributions proportional to *g*<sub>*E**W*</sub><sup>4</sup>*v*<sup>2</sup> < *m**a**t**h* > *w**h**e**r**e* < *m**a**t**h* > *g*<sub>*E**W*</sub> stands for the electroweak gauge coupling; these are hence subdominant to the contributions from $SSV, FFV, \\overline{FF}V$ diagrams involving the electroweak gauge bosons (which we are also neglecting) which would be proportional to *g*<sub>*E**W*</sub><sup>2</sup>*v*<sup>2</sup> < *m**a**t**h* > .*N**o**t**e*, *f**o**r**c**o**n**s**i**s**t**e**n**c**y*, *S**A**R**A**H**a**l**s**o**s**e**t**s**a**l**l**g**a**u**g**e**c**o**u**p**l**i**n**g**s**a**r**i**s**i**n**g**i**n**t**h**e* < *m**a**t**h* > *D*-terms of broken groups in the vertices to zero. The masses used in the loops are tree-level masses calculated from running *D**R*′ parameters. In this context, there are two possibilities to treat *D*-term contributions to the tree-level masses: either one can work in the gaugeless limit where these contributions are also put to zero, or one can work with the full tree-level masses as this is also done in diagrammatic calculations. SARAH offers both possibilities. In the gaugeless limit the *S**U*(2)<sub>*L*</sub> × *U*(1)<sub>*Y*</sub> gauge symmetries become global symmetries. Therefore, it is obvious that no gauge dependence has been introduced by including only Goldstone diagrams but no diagrams of the corresponding vector bosons. Of course, when including *D*-terms in the mass matrices the derivatives of the *D*-terms are still forced to vanish.
|
|
|
|
The remaining topologies are those which have been considered so far in the MSSM to obtain the dominant two-loop corrections and which are implemented in public computer tools. The impact on the Higgs mass is considered to be moderate when neglecting contributions propotional to the electroweak gauge couplings in models with the SM gauge sector, since they are significantly smaller than the strong and top Yukawa coupling – and the diagrams involving these couplings are of typically lower multiplicity. In fact, by inspecting the form of the loop functions it is evident that the topologies *S**V*, *V**V*, *V**V**V*, *V**V**S* < *m**a**t**h* > *a**n**d* < *m**a**t**h* > *G**G**V* lead to contributions proportional to *g*<sub>*E**W*</sub><sup>4</sup>*v*<sup>2</sup> < *m**a**t**h* > *w**h**e**r**e* < *m**a**t**h* > *g*<sub>*E**W*</sub> stands for the electroweak gauge coupling; these are hence subdominant to the contributions from $`SSV, FFV, \overline{FF}V`$ diagrams involving the electroweak gauge bosons (which we are also neglecting) which would be proportional to *g*<sub>*E**W*</sub><sup>2</sup>*v*<sup>2</sup> < *m**a**t**h* > .*N**o**t**e*, *f**o**r**c**o**n**s**i**s**t**e**n**c**y*, *S**A**R**A**H**a**l**s**o**s**e**t**s**a**l**l**g**a**u**g**e**c**o**u**p**l**i**n**g**s**a**r**i**s**i**n**g**i**n**t**h**e* < *m**a**t**h* > *D*-terms of broken groups in the vertices to zero. The masses used in the loops are tree-level masses calculated from running *D**R*′ parameters. In this context, there are two possibilities to treat *D*-term contributions to the tree-level masses: either one can work in the gaugeless limit where these contributions are also put to zero, or one can work with the full tree-level masses as this is also done in diagrammatic calculations. SARAH offers both possibilities. In the gaugeless limit the *S**U*(2)<sub>*L*</sub> × *U*(1)<sub>*Y*</sub> gauge symmetries become global symmetries. Therefore, it is obvious that no gauge dependence has been introduced by including only Goldstone diagrams but no diagrams of the corresponding vector bosons. Of course, when including *D*-terms in the mass matrices the derivatives of the *D*-terms are still forced to vanish.
|
|
|
|
|
|
|
|
For the calculation of the two-loop effective potential the expressions of Ref. given in two-component notation have been translated into four-component language. All necessary generic expressions have been implemented in SARAH. SARAHuses these expressions to generate `Fortran`code for all two-loop diagrams which are possible in the considered model assuming the topologies *S**S*, *S**S**V*, *S**S**S*, *F**F**S*, $\\overline{FF}S$, *F**F**V* and $\\overline{FF}V$.
|
|
|
|
For the calculation of the two-loop effective potential the expressions of Ref. given in two-component notation have been translated into four-component language. All necessary generic expressions have been implemented in SARAH. SARAHuses these expressions to generate `Fortran`code for all two-loop diagrams which are possible in the considered model assuming the topologies *S**S*, *S**S**V*, *S**S**S*, *F**F**S*, $`\overline{FF}S`$, *F**F**V* and $`\overline{FF}V`$.
|
|
|
|
|
|
|
|
### Numerical derivation
|
|
|
|
|
| ... | ... | @@ -77,10 +70,7 @@ As soon as the two-loop effective potential is calculated, one can obtain the tw |
|
|
|
1. *'Purely numerical derivation:* in this approach the entire potential is derived with respect to the VEVs.
|
|
|
|
2. **Semi-analytical derivation:** in this approach the derivatives of all masses and couplings with respect to the VEVs are calculated separately also in a numerical way. However, all one- and two-loop derivatives of the loop-functions with respect to their arguments have been calculated analytically and implemented in the output SPhenocode. The derivatives of the potential are then calculated combining both results using the chain rule. This can be easily done because every contribution to the potential is a product of couplings (*c*<sub>1</sub>, *c*<sub>2</sub>), masses (*m*<sub>*i*</sub>) and a loop function *f*<sub>*X*</sub> with a coefficient *k*:
|
|
|
|
|
|
|
|
$\\begin{aligned}
|
|
|
|
V^{(2)}_X &=& k\\cdot (c_1 c_2) \\cdot f_{X}(m_1^2,m_2^2,m_3^2), \\quad \\text{for } X=FFS,FFV,SSV\\\\
|
|
|
|
V^{(2)}_X &=& k\\cdot (c_1 c_2) \\cdot m_{F1} m_{F2} \\cdot f_{X}(m_{F1}^2,m_{F2}^2,m_3^2), \\quad \\text{for } X=\\overline{FFS},\\overline{FFV}\\\\
|
|
|
|
V^{(2)}_X &=& k\\cdot (c_1) \\cdot f_{X}(m_1^2,m_2^2), \\quad \\text{for } X=SS\\end{aligned}$
|
|
|
|
$` V^{(2)}_X = k\cdot (c_1 c_2) \cdot f_{X}(m_1^2,m_2^2,m_3^2), \quad \text{for } X=FFS,FFV,SSV\\ V^{(2)}_X = k\cdot (c_1 c_2) \cdot m_{F1} m_{F2} \cdot f_{X}(m_{F1}^2,m_{F2}^2,m_3^2), \quad \text{for } X=\overline{FFS},\overline{FFV}\\ V^{(2)}_X = k\cdot (c_1) \cdot f_{X}(m_1^2,m_2^2), \quad \text{for } X=SS`$
|
|
|
|
|
|
|
|
The second method is numerically slightly more expensive but it is also more stable. In particular, in the presence of large hierarchies in the VEVs the purely numerical method could become inaccurate.
|
|
|
|
|
| ... | ... | @@ -89,7 +79,7 @@ Diagrammatic calculation |
|
|
|
|
|
|
|
A fully diagrammatic calculation for two-loop contributions to scalar self-energies with SARAH –SPheno became available with Ref. . In this setup a new set of generic expressions is used. The following two-loop diagrams are included in the limit *p*<sup>2</sup> = 0:
|
|
|
|
|
|
|
|
[zentriert](/Datei:2-loop_diagrammatic.png "wikilink")
|
|
|
|

|
|
|
|
|
|
|
|
These are again the diagrams which don’t vanish in general in the gaugeless limit. The results of Ref. have the advantage that the expressions which are derived from the effective potential are much simpler than taking the limit *p*<sup>2</sup> → 0 in other two-loop functions available in literature. The diagrammatic method gives completely equivalent results to the effective potential calculation but is usually numerically more robust and it is now the default method. [One can switch in SPheno easily between the diagrammatic and effective potential calculation.](/Using_SPheno_for_two-loop_masses "wikilink")
|
|
|
|
|
| ... | ... | |
| ... | ... | |